Project Overview
In this project, we extended the ray tracer from the previous project and added BSDF/BRDF functions for various other materials to implement refraction and reflection behaviors of objects interacting with rays. We implemented the bidirectional scattering distribution functions for mirror and glass surfaces in the first part. Then in part two, we worked on implementing the bidirectional reflectance distribution function for microfacet models. For part three, we added a new light source in the form of infinite light and sourced light samples from an exr file with a background environment map. And finally in part four, we worked on camera simulation topics by manipulating focal distance and aperture on the renders and simulating thin lenses. Overall, the project left us with a functional renderer and ray tracer built up from the start of tracing individual rays and calculating intersections, all the way to tracing and manipulating rays through lenses to simulate camera abilities.
Part 1: Ray Generation and Intersection
To expand on my overview of part 1, we started by implementing reflection. This was a rather trivial task, given that we knew we were simply reflecting over the z normal axis. To do this, I just flipped the direction of the x and y components of the incoming direction and stored them in the outgoing direction. This scatter is a complete reflection of light in the outgoing direction. To make use of the reflect function, we wrote the sample_f function of the MirrorBSDF, where we set the pdf to 1 because of our complete reflection, and then return the reflectance/cos(theta) to output the appropriate spectrum. We were told to run with a maximum ray depth greater than 1 because if we only ran it with ray depth of 1, the ray would intersect the object, but would never reflect because the ray would terminate immediately after reflection.
To implement refraction, we used the parameters of the index of refraction, used the direction of the rays to determine if we were entering or exiting the mediums, and then calculated eta accordingly. By usign snell's law with the appropriate eta values, we could determine when refraction occurred and store the new ray direction accordingly. And finally, we implemented the scattering distribution function for glass. When doing this, we introduced a randomness factor based on Schlick's reflection coefficient, which was then assigned to the pdf. Schlick's coefficient determined whether there was reflection or refraction for the outgoing direction. We also accounted for total internal reflection and only accounted for reflection and not refraction in that scenario.
The results from Part 1

|

|

|

|

|

|

|
Something neat is the multibounce effects that appeat in each image. When we have 5 rays, you can see the partial reflection of the right sphere on the blue wall. 0 obviously has no objects, 1 doesn't illuminate the spheres past intersection, and 2 rays stuggles to move through the transparent sphere. We get better reflections of the glass sphere in the mirror sphere as the rays increase, and rays=100 seems to be the best, although it doesn'tlook that much better than rays=5.
Part 2: Microfacet Materials
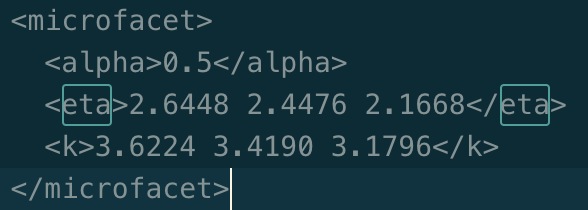
The microfacet model moves us beyond standard surfaces and glass/mirrors. Instead, we now have the ability to perform reflection and refraction over conductive surfaces defined by their eta and k values. Some of the materials we rendered were gold, aluminum, silver and copper. The first step was to evaluate the Microfacet Bidirectional Reflectance Distribution Function. The BRDF for this was defined as the Fresnel term * the shadowing-masking term * the normal distribution function, all divided by a factor of the surface normal dotted with the incoming and outgoing ray directions. The Fresnel Term and the Normal Distribution Function were written in the next two steps. The NDF was a function of the angle between the half vector and the surface normal and the roughness of the surface. The roughness was represented by an alpha value, where the smaller the value, the smoother the surface. The Fresnel term for microfacet materials is different from the mirror/glass functions because it differs for air-dielectric materials and air-conductor materials. Metals are air-conductors. The Fresnel term formula was a function of the eta and k values for a particular metal, and the angle of incidence. Finally, we implemented importance sampling for the sampling function, to overwrite the cosine-hemisphere sampling function that was included. We wanted to sample the BRDF according to the Beckmann distribution function, so we used the given pdfs for the angles phi and theta to reduce noise and then finish by using the inversion method to "look up" values given their pdf.
Below is the result of the CBdragon_microfacet_au.dae with varying alpha values. Sampling rate was 256, max_ray_depth=7, and 4 light samples. It is clear to see that as the alpha value drops, the dragon quickly becomes much smoother and significantly more reflective.

|

|

|

|
To compare the cosine hemisphere sampling to the importance sampling: Sample Rate=64, 1 light sample, max_ray_depth=5. The difference is clear to see here, that the bunny in importance sampling is rendered much less noisily, and the reason is explained because the cosine hemisphere doesn't appropriately assign the pdf, because the microfacet model uses the Beckmann NDF, so it would be better and less noisy to have pdfs that actively resemble the Beckmann distribution function.

|

|
For my other conductor metal, I used Vanadium-galloum alloy, primarily because it sounded cool. I took the rgb wavelengths and calculated the eta and k values for each color channel. The wavelengths were given as follows: 614 nm (red), 549549 nm (green) and 466466 nm (blue). An example of the blue channel. Sampling rate=64, 4 light samples, max_ray_depth=5.


Part 3: Environment Light
Infinte Environment Light is a type of light that radiates from all directions, giving us a feeling of outdoor type lighting. We get these values from .exr files, which are hdr type files, and the texture map is parameterized with phi and theta angles. We were given helper functions to convert phi and theta in to xy coordinates, and the inverse as well. To sample the directions, we could use the helper functions to convert directon vectors into xy coordinates, and then use the given bilinear interpolation function to actually index into the best spot in the environment map. Uniform sampling was quite easy to implement and all we had to do was sample from the randomly selected direction and then assign the distance to light and the pdf. The pdf was 1/4*pi because of the shape of the sphere. Environment lighting works because we develop cumulative and probability distributions from the environment map we take as an input. And then we sample according to the probabilities we compute, for both the conditional and marginal probabilities, and we can use these in the exact same manner as the inversion method from Part 2, to reverse index from a pdf to a given environment map value to sample lighting. From an infinte light source like environment lighting, we can theoretically sample everything, but sampling based on the probability distribution functions of the environment map gives us a more effective and efficient method of environment lighting.
The probability_debug image for field.exr resembles that of the spec.
For all four of the images below, the sample rate was 4 and there were 64 samples per light.

|

|
In the ordinary bunny, its a little difficult to tell the differences in noise, but the importance bunny looks measurably less granier than the uniform bunny.

|

|
The difference in noise in the microfacet bunny is evident in the cheeks and near the feet, where it's clear that the importance sampling gave us more valuable locations to sample the light from.
Part 4: Depth of Field
This was probably my favorite part of the project, given how much it related to photography concepts and modeling cameras in graphics. Given the ray diagram from the spec, I used the ray-plane intersection formulas and the knowledge of the z point on the plane to compute the t value for the time of intersection. Then, I used the t value to compute the x and y points of intersection on the z plane of the focal distance, and this enabled me to calculate the new ray that mapped to the same location as the ray through the origin. In the pinhole camera, every ray of light that came in through the pinhole, was projected onto the screen and without any lens warping or transformations. Meanwhile with the thin lens of a given radius, we are "mapping" the rays from where they would have gone in the pinhole setting, to different samples on the lens. With a finite aperture, the depth of field becomes measurable and focal distances start to matter. In theory, a pinhole camera has an infinte aperture and therefore a full depth of field in which everything appears in focus. As the aperture size increases, the depth of field decreases because of the nature of rays traveling through thin lenses.
I built a gif of my focus stack and my aperture stack, but to see the details of each frame, just look to the table below.
The focus stack, with focal distance ranging from 2.1 to 3.1 in increments of 0.2.
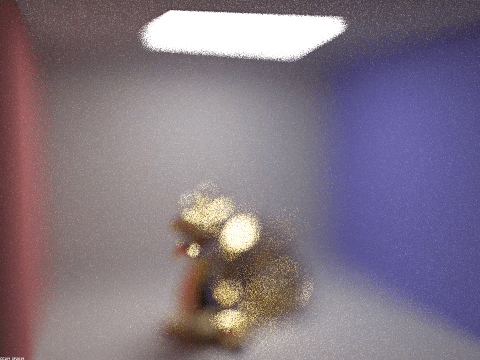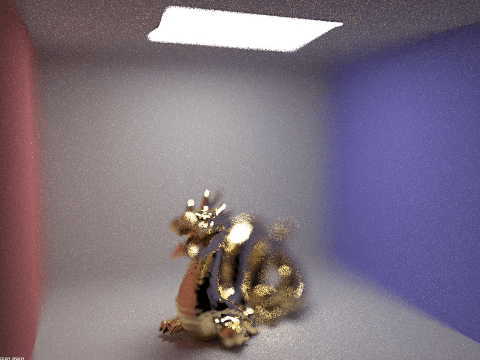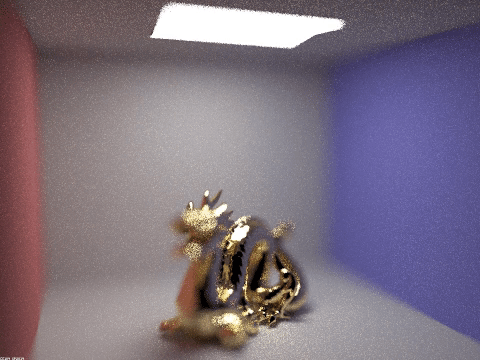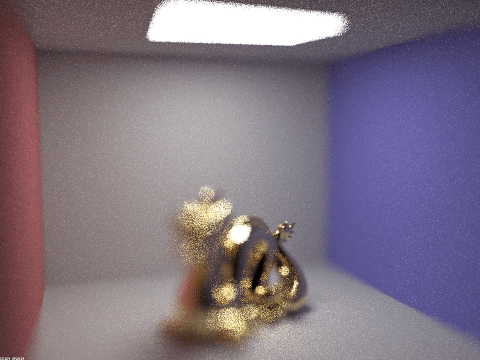
The aperture stack with lens radius ranging from 0.01 to 1.5. It's neat to notice here how the center of the dragon, at approximately focal distance 2.7, stays in focus through all thr frames, demonstrating the effects of the depth of field.

The detailed version of the distance stack: Sample rate=32, light samples=4, aperture =.25
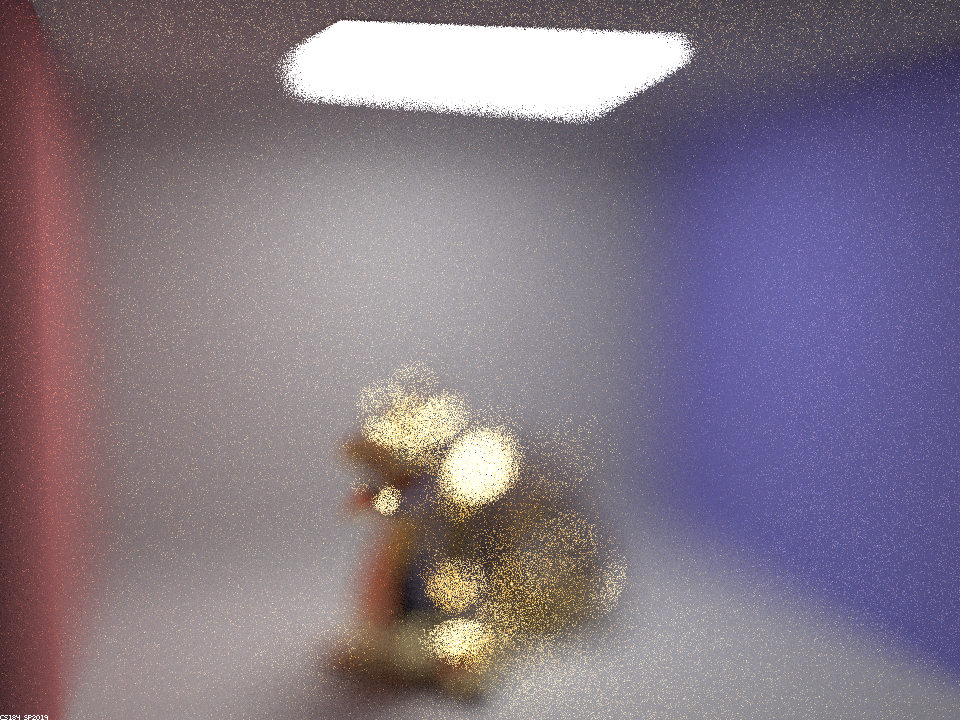
|
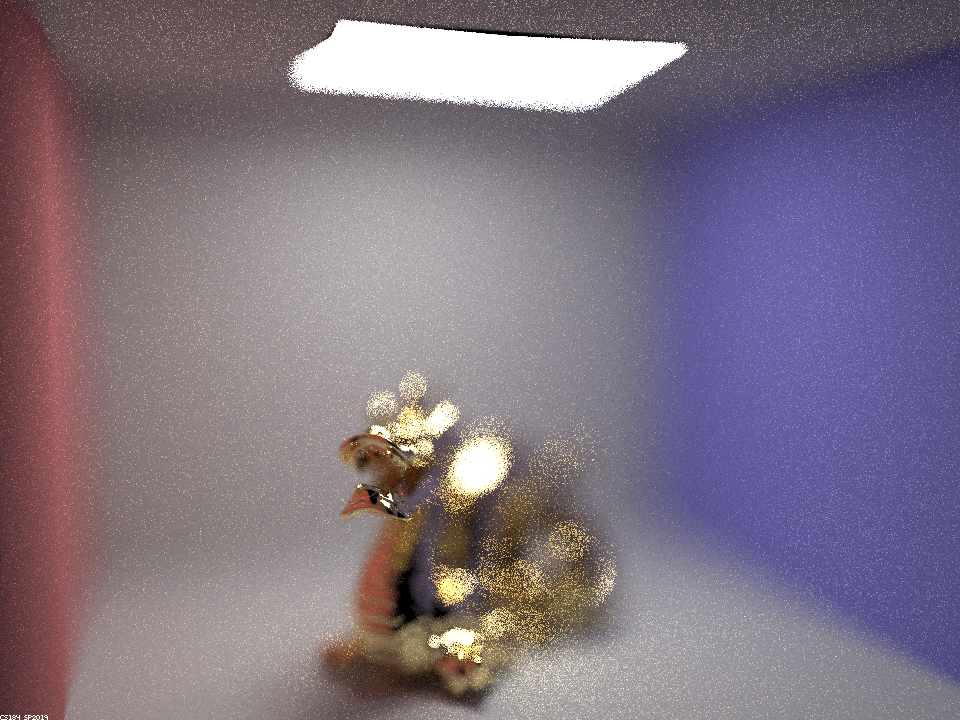
|

|

|

|

|
The detailed version of the aperture stack. sample rate=32, light samples=4, focal distance=2.7

|

|

|

|
|

|
The lens radius works in inverse to the measurements of a camera's aperture, in this scenario, the smaller the radius, the smaller the physical aperture, meaning the larger the depth of field. As we shrink the radius to infinity, we would get infinite depth of fields as seen before implementing the lens equations. However in reality, we cannot do this because tiny holes only let in very little amounts of light, and sensors cannot process such small amounts of light without adding significant noise to the image.